Ideas, medidas y formas a la hora de diseñar una cocina funcional
martes, 28 de abril de 2020
viernes, 24 de abril de 2020
Obtención de las vistas de un objeto
Generalidades
Se denominan vistas principales de un objeto, a las proyecciones ortogonales del mismo sobre 6 planos, dispuestos en forma de cubo. También se podría definir las vistas como, las proyecciones ortogonales de un objeto, según las distintas direcciones desde donde se mire.
Las reglas a seguir para la representación de las vistas de un objeto, se recogen en la norma UNE 1-032-82, «Dibujos técnicos: Principios generales de representación», equivalente a la norma ISO 128-82.
Denominación de las vistas
Si situamos un observador según las seis direcciones indicadas por las flechas, obtendríamos las seis vistas posibles de un objeto.
Estas vistas reciben las siguientes denominaciones:

Vista A: Vista de frente o alzado
Vista B: Vista superior o planta
Vista C: Vista derecha o lateral derecha
Vista D: Vista izquierda o lateral izquierda
Vista E: Vista inferior
Vista F: Vista posterior
Posiciones relativas de las vistas
Para la disposición de las diferentes vistas sobre el papel, se pueden utilizar dos variantes de proyección ortogonal de la misma importancia:
El método de proyección del primer diedro, también denominado Europeo (antiguamente, método E)
El método de proyección del tercer diedro, también denominado Americano (antiguamente, método A)
En ambos métodos, el objeto se supone dispuesto dentro de un cubo, sobre cuyas seis caras, se realizarán las correspondientes proyecciones ortogonales del mismo.
La diferencia estriba en que, mientras en el sistema Europeo, el objeto se encuentra entre el observador y el plano de proyección, en el sistema Americano, es el plano de proyección el que se encuentra entre el observador y el objeto.

El desarrollo del cubo de proyección, nos proporciona sobre un único plano de dibujo, las seis vistas principales de un objeto, en sus posiciones relativas.
Con el objeto de identificar, en que sistema se ha representado el objeto, se debe añadir el símbolo que se puede apreciar en las figuras, y que representa el alzado y vista lateral izquierda, de un cono truncado, en cada uno de los sistemas.
Una vez realizadas las seis proyecciones ortogonales sobre las caras del cubo, y manteniendo fija, la cara de la proyección del alzado (A), se procede a obtener el desarrollo del cubo, que como puede apreciarse en las figuras, es diferente según el sistema utilizado.

El desarrollo del cubo de proyección, nos proporciona sobre un único plano de dibujo, las seis vistas principales de un objeto, en sus posiciones relativas.
Con el objeto de identificar, en que sistema se ha representado el objeto, se debe añadir el símbolo que se puede apreciar en las figuras, y que representa el alzado y vista lateral izquierda, de un cono truncado, en cada uno de los sistemas.

Correspondencia entre las vistas
Como se puede observar en las figuras anteriores, existe una correspondencia obligada entre las diferentes vistas. Así estarán relacionadas:
El alzado, la planta, la vista inferior y la vista posterior, coincidiendo en anchuras.
El alzado, la vista lateral derecha, la vista lateral izquierda y la vista posterior, coincidiendo en alturas.
La planta, la vista lateral izquierda, la vista lateral derecha y la vista inferior, coincidiendo en profundidad.
Habitualmente con tan solo tres vistas, el alzado, la planta y una vista lateral, queda perfectamente definida una pieza. Teniendo en cuenta las correspondencias anteriores, implicarían que dadas dos cualquiera de las vistas, se podría obtener la tercera, como puede apreciarse en la figura:

También, de todo lo anterior, se deduce que las diferentes vistas no pueden situarse de forma arbitraria. Aunque las vistas aisladamente sean correctas, si no están correctamente situadas, no definirán la pieza.

Se denominan vistas principales de un objeto, a las proyecciones ortogonales del mismo sobre 6 planos, dispuestos en forma de cubo. También se podría definir las vistas como, las proyecciones ortogonales de un objeto, según las distintas direcciones desde donde se mire.
Las reglas a seguir para la representación de las vistas de un objeto, se recogen en la norma UNE 1-032-82, «Dibujos técnicos: Principios generales de representación», equivalente a la norma ISO 128-82.
Denominación de las vistas
Si situamos un observador según las seis direcciones indicadas por las flechas, obtendríamos las seis vistas posibles de un objeto.
Estas vistas reciben las siguientes denominaciones:

Vista A: Vista de frente o alzado
Vista B: Vista superior o planta
Vista C: Vista derecha o lateral derecha
Vista D: Vista izquierda o lateral izquierda
Vista E: Vista inferior
Vista F: Vista posterior
Posiciones relativas de las vistas
Para la disposición de las diferentes vistas sobre el papel, se pueden utilizar dos variantes de proyección ortogonal de la misma importancia:
El método de proyección del primer diedro, también denominado Europeo (antiguamente, método E)
El método de proyección del tercer diedro, también denominado Americano (antiguamente, método A)
En ambos métodos, el objeto se supone dispuesto dentro de un cubo, sobre cuyas seis caras, se realizarán las correspondientes proyecciones ortogonales del mismo.
La diferencia estriba en que, mientras en el sistema Europeo, el objeto se encuentra entre el observador y el plano de proyección, en el sistema Americano, es el plano de proyección el que se encuentra entre el observador y el objeto.

El desarrollo del cubo de proyección, nos proporciona sobre un único plano de dibujo, las seis vistas principales de un objeto, en sus posiciones relativas.
Con el objeto de identificar, en que sistema se ha representado el objeto, se debe añadir el símbolo que se puede apreciar en las figuras, y que representa el alzado y vista lateral izquierda, de un cono truncado, en cada uno de los sistemas.
Una vez realizadas las seis proyecciones ortogonales sobre las caras del cubo, y manteniendo fija, la cara de la proyección del alzado (A), se procede a obtener el desarrollo del cubo, que como puede apreciarse en las figuras, es diferente según el sistema utilizado.

El desarrollo del cubo de proyección, nos proporciona sobre un único plano de dibujo, las seis vistas principales de un objeto, en sus posiciones relativas.
Con el objeto de identificar, en que sistema se ha representado el objeto, se debe añadir el símbolo que se puede apreciar en las figuras, y que representa el alzado y vista lateral izquierda, de un cono truncado, en cada uno de los sistemas.

Correspondencia entre las vistas
Como se puede observar en las figuras anteriores, existe una correspondencia obligada entre las diferentes vistas. Así estarán relacionadas:
El alzado, la planta, la vista inferior y la vista posterior, coincidiendo en anchuras.
El alzado, la vista lateral derecha, la vista lateral izquierda y la vista posterior, coincidiendo en alturas.
La planta, la vista lateral izquierda, la vista lateral derecha y la vista inferior, coincidiendo en profundidad.
Habitualmente con tan solo tres vistas, el alzado, la planta y una vista lateral, queda perfectamente definida una pieza. Teniendo en cuenta las correspondencias anteriores, implicarían que dadas dos cualquiera de las vistas, se podría obtener la tercera, como puede apreciarse en la figura:

También, de todo lo anterior, se deduce que las diferentes vistas no pueden situarse de forma arbitraria. Aunque las vistas aisladamente sean correctas, si no están correctamente situadas, no definirán la pieza.

Etiquetas:
Arquitectura,
dibujo técnico
Escala y Proporción en arquitectura
Escala y proporción explicada con peras y manzanas
Se trata de dos conceptos clave para la arquitectura, que sólo pueden aprenderse conforme se explora el mundo del espacio y sus relaciones.

Estos dos términos son la base del trabajo del arquitecto. Si bien ambas están relacionadas con el tamaño de las cosas, representan dos conceptos diferentes.
Para distinguirlas usaremos algunos ejemplos.
La escala se refiere al tamaño de un objeto cualquiera en relación con otro.

Un árbol tiene una escala determinada respecto a un ser humano; el ser humano posee una escala que se usa para establecer el tamaño de las cosas en relación a su cuerpo.
La proporción va en función de la relación entre las partes y un todo; tiene que ver con un objeto en sí mismo.

Piensa en un rostro humano: ojos, nariz, y boca mantienen un equilibrio respecto del todo, una proporción adecuada; de lo contrario, una cara deforme causa inquietud o desequilibrio.
Las figuras geométricas como el cuadrado o el rectángulo dependen de la proporción para que podamos identificarlas como tales; lo mismo pasa con el círculo. La excepción es el triángulo, una figura indeformable.

El David de Miguel Ángel, por ejemplo, alcanza los 4 metros de altura pero en sí mismo mantiene una proporción adecuada a la hora de contemplarse (aunque es verdad que Miguel Ángel deformó ciertas partes porque los espectadores lo aprecian desde abajo).

Sin embargo, aunque está debidamente proporcionado, el David está fuera de escala, pues ningún hombre mide lo mismo que la estatua.
Como verás, salirse de escala puede estar justificado, pero hay que saber hacerlo.
El Jardín de Esculturas de Minneapolis, ubicado frente al Centro de Arte Walker, fue diseñado por el arquitecto Edward Larrabee Barnes. En este espacio hay una escultura llamada Spoonbridge & Cherry (1988), obra de Coosje van Bruggen.
En este caso, tanto la cuchara y la cereza están proporcionadas, pues mantienen una relación armónica entre sus partes. Por el contrario están fuera de escala, pues ninguna cuchara que sea útil mide lo que esta obra plástica. Lo mismo pasa con la cereza.(1)
La proporción en arquitectura busca crear un sistema armonioso basado en una medida que se repite una y otra vez para darle sentido al conjunto.
El cuerpo humano, por ejemplo, que suele usarse como base de los sistemas de proporción. En términos generales, la cabeza de un hombre mide aproximadamente 1/8 de la altura del cuerpo, y la distancia de los brazos extendidos será muy aproximada a la altura del cuerpo. (2)
La arquitectura clásica llevó muy lejos la idea de que la divinidad se manifestaba en una serie de números cuyo origen estaba ligado a la naturaleza o a la divinidad.
El número de oro, la sección áurea o el Modulor son sistemas para darle proporción a la arquitectura mediante las relaciones que establecen entre las partes de un todo.
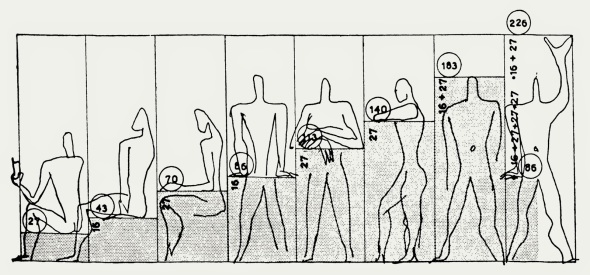
Podría decirse que la proporción es más un juego matemático de números y sus relaciones entre sí y que la escala es más una apreciación derivado de la experiencia cotidiana que nos permite reconocer el tamaño relativo de personas, árboles, insectos, perros, etc.
En los edificios, el cuerpo humano es la referencia principal, y que sirve de base para establecer el tamaño de puertas, ventanas, la altura del techo y demás detalles en comparación con nuestro propio tamaño y con respecto a las demás.
El manejo de la escala y la proporción de un edificio es de vital importancia para que los usuarios no se sientan vacíos dentro de un espacio muy alto o muy profundo, o en un sitio estrecho y bajo.

Por ello, pueden haber edificios bien proporcionados pero fuera de escala, sobre todo cuando impactan un contexto.
Imaginemos una torre de cien pisos en un barrio donde todas las demás construcciones cuentan con un nivel. ¿Qué pasa? El edificio está fuera de escala respecto de lo que lo rodea.

Sin embargo, si la torre de 100 pisos se plantea de tal forma que su escala se adapte a las construcciones de un nivel podría mantener el equilibrio entre sí y lo que le rodea.
Jugar con estos dos conceptos da como resultado un edificio armonioso y bello. Todo depende de su correcta aplicación para crear arquitectura.
Referencias:
1- Claes Oldenburg & Coosje van Bruggen: Exhibitions & Projects: Spoonbridge and Cherry. (s.f.). Recuperado 7 febrero, 2020, de oldenburgvanbruggen.com/largescaleprojects/spoonbridge.htm
2 - Donnal6696 (2018, 6 septiembre). Proportion and Scale | Their application in Architecture - Bruce Donnally. Recuperado 7 febrero, 2020, de donnallyarchitects.com/proportion-and-scale/
FUENTE:https://noticias.arq.com.mx/
Se trata de dos conceptos clave para la arquitectura, que sólo pueden aprenderse conforme se explora el mundo del espacio y sus relaciones.

Estos dos términos son la base del trabajo del arquitecto. Si bien ambas están relacionadas con el tamaño de las cosas, representan dos conceptos diferentes.
Para distinguirlas usaremos algunos ejemplos.
La escala se refiere al tamaño de un objeto cualquiera en relación con otro.

Un árbol tiene una escala determinada respecto a un ser humano; el ser humano posee una escala que se usa para establecer el tamaño de las cosas en relación a su cuerpo.
La proporción va en función de la relación entre las partes y un todo; tiene que ver con un objeto en sí mismo.

Piensa en un rostro humano: ojos, nariz, y boca mantienen un equilibrio respecto del todo, una proporción adecuada; de lo contrario, una cara deforme causa inquietud o desequilibrio.
Las figuras geométricas como el cuadrado o el rectángulo dependen de la proporción para que podamos identificarlas como tales; lo mismo pasa con el círculo. La excepción es el triángulo, una figura indeformable.

El David de Miguel Ángel, por ejemplo, alcanza los 4 metros de altura pero en sí mismo mantiene una proporción adecuada a la hora de contemplarse (aunque es verdad que Miguel Ángel deformó ciertas partes porque los espectadores lo aprecian desde abajo).

Sin embargo, aunque está debidamente proporcionado, el David está fuera de escala, pues ningún hombre mide lo mismo que la estatua.
Como verás, salirse de escala puede estar justificado, pero hay que saber hacerlo.
El Jardín de Esculturas de Minneapolis, ubicado frente al Centro de Arte Walker, fue diseñado por el arquitecto Edward Larrabee Barnes. En este espacio hay una escultura llamada Spoonbridge & Cherry (1988), obra de Coosje van Bruggen.
En este caso, tanto la cuchara y la cereza están proporcionadas, pues mantienen una relación armónica entre sus partes. Por el contrario están fuera de escala, pues ninguna cuchara que sea útil mide lo que esta obra plástica. Lo mismo pasa con la cereza.(1)
La proporción en arquitectura busca crear un sistema armonioso basado en una medida que se repite una y otra vez para darle sentido al conjunto.
El cuerpo humano, por ejemplo, que suele usarse como base de los sistemas de proporción. En términos generales, la cabeza de un hombre mide aproximadamente 1/8 de la altura del cuerpo, y la distancia de los brazos extendidos será muy aproximada a la altura del cuerpo. (2)
La arquitectura clásica llevó muy lejos la idea de que la divinidad se manifestaba en una serie de números cuyo origen estaba ligado a la naturaleza o a la divinidad.
El número de oro, la sección áurea o el Modulor son sistemas para darle proporción a la arquitectura mediante las relaciones que establecen entre las partes de un todo.

Podría decirse que la proporción es más un juego matemático de números y sus relaciones entre sí y que la escala es más una apreciación derivado de la experiencia cotidiana que nos permite reconocer el tamaño relativo de personas, árboles, insectos, perros, etc.
En los edificios, el cuerpo humano es la referencia principal, y que sirve de base para establecer el tamaño de puertas, ventanas, la altura del techo y demás detalles en comparación con nuestro propio tamaño y con respecto a las demás.
El manejo de la escala y la proporción de un edificio es de vital importancia para que los usuarios no se sientan vacíos dentro de un espacio muy alto o muy profundo, o en un sitio estrecho y bajo.

Por ello, pueden haber edificios bien proporcionados pero fuera de escala, sobre todo cuando impactan un contexto.
Imaginemos una torre de cien pisos en un barrio donde todas las demás construcciones cuentan con un nivel. ¿Qué pasa? El edificio está fuera de escala respecto de lo que lo rodea.

Sin embargo, si la torre de 100 pisos se plantea de tal forma que su escala se adapte a las construcciones de un nivel podría mantener el equilibrio entre sí y lo que le rodea.
Jugar con estos dos conceptos da como resultado un edificio armonioso y bello. Todo depende de su correcta aplicación para crear arquitectura.
Referencias:
1- Claes Oldenburg & Coosje van Bruggen: Exhibitions & Projects: Spoonbridge and Cherry. (s.f.). Recuperado 7 febrero, 2020, de oldenburgvanbruggen.com/largescaleprojects/spoonbridge.htm
2 - Donnal6696 (2018, 6 septiembre). Proportion and Scale | Their application in Architecture - Bruce Donnally. Recuperado 7 febrero, 2020, de donnallyarchitects.com/proportion-and-scale/
FUENTE:https://noticias.arq.com.mx/
Etiquetas:
Arquitectura,
escala,
proporción
Suscribirse a:
Comentarios (Atom)























